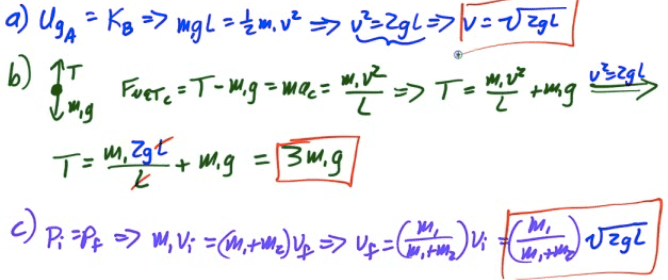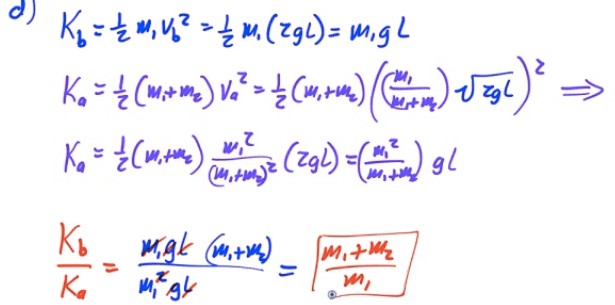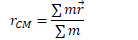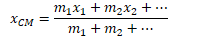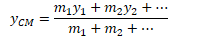Center of Mass
Real objects are more complex than theoretical particles
Treat entire object as if its entire mass were contained at a single point known as the object's center of mass (CM)
Center of mass is the weighted average of the location of mass in an object
Find CM by Inspection
For uniform density objects, CM is the geometric center
For objects with multiple parts, find CM of each part and treat as a point
For irregular objects, suspend object from two or more points and drop a plumb line. The line intersects at the center of mass
Calculating CM for Systems of Particles
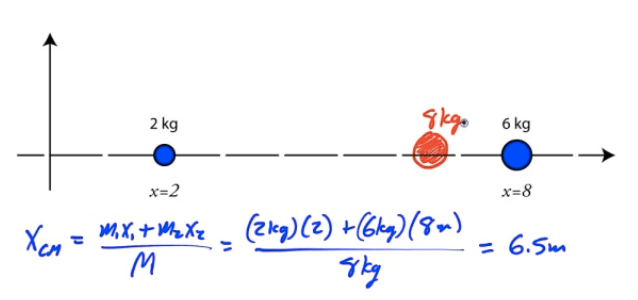
Example 1: Center of Mass (1D)
Example 2: CM of Continuous System
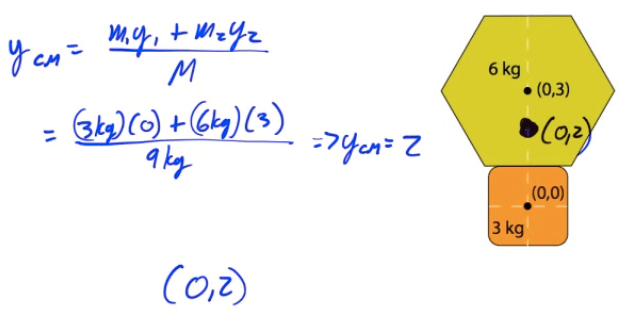
Example 3: Center of Mass (2D)
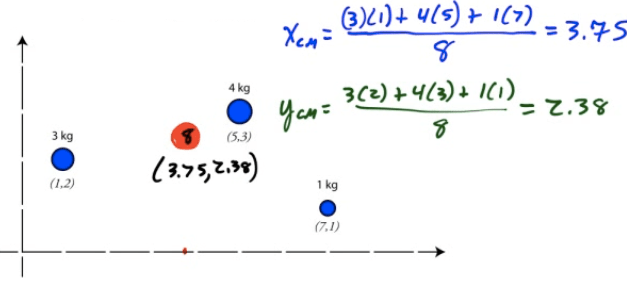
Finding CM by Integration
For more complex objects, you can find the center of mass by summing up all the little pieces of position vectors multiplied by the differential of mass and dividing by the total mass
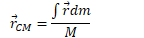
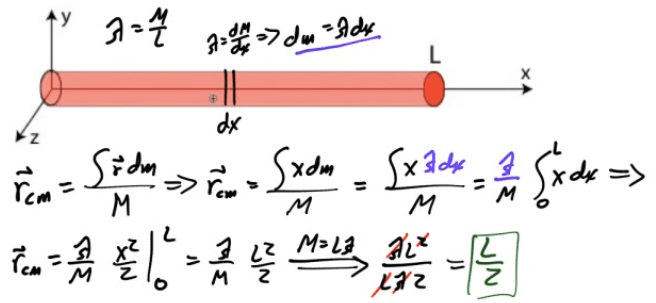
Example 4: CM of a Uniform Rod
Example 5: CM of a Non-Uniform Rod
Find the center of mass of a non-uniform rod of length L and mass M whose density is given by λ=kx

Center of Mass Relationships

Center of Gravity
Center of Gravity refers to the location at which the force of gravity acts upon an object as if it were a point particle with all its mass focused at that point
In a uniform gravitational field, Center of Gravity and Center of Mass are the same
In a non-uniform gravitational field, they may be different
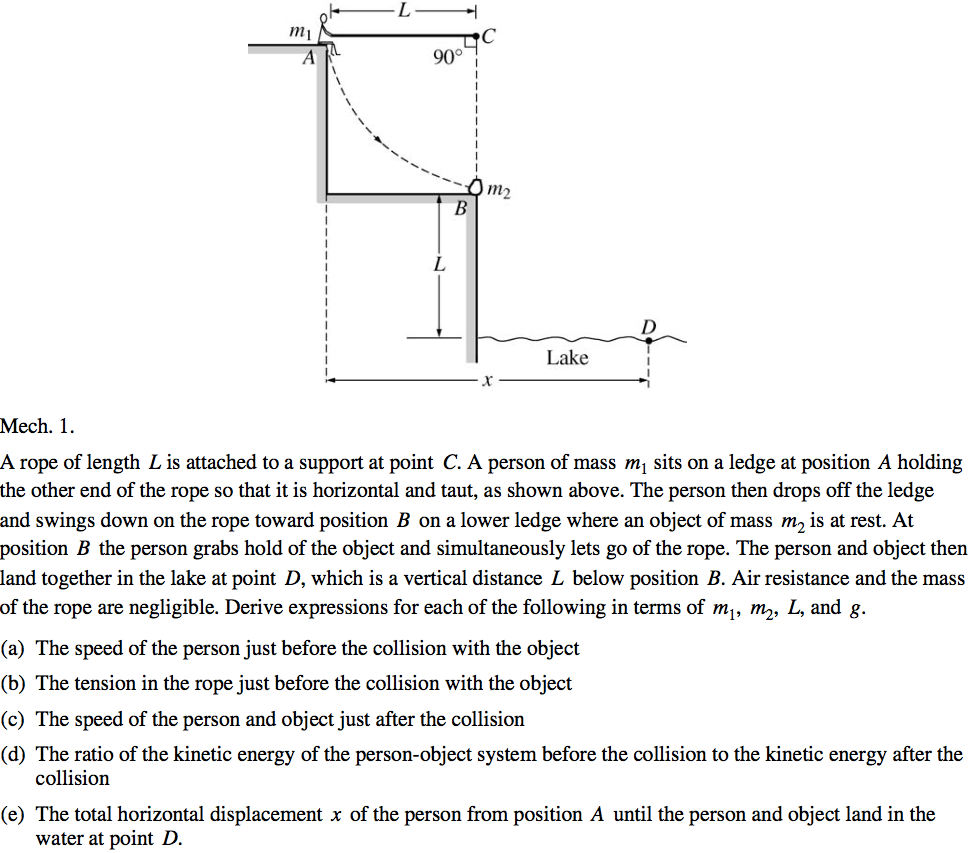
2004 Free Response Question 1